Sifting through refractive formulas

There are more of them, serving different purposes, all striving for the same goal: excellent vision.

By Sumitra S. Khandelwal, MD, and Douglas D. Koch, MD

Today’s cataract surgery patients are younger when they want this surgery, and are having it at a younger age than previous generations. Moreover, when these patients desire a target focal point without spectacles, they expect that desire to be fulfilled. These patients are perhaps lucky to be living in a time in which surgical techniques have improved, along with measurements of corneal power, astigmatism and lens calculations. But, there is a but.

Third and fourth generation formulas

Despite the new technologies available, the choice of which lens to place still hinges on a formula that estimates the IOL’s refractive power in the eye based on the IOL’s location, or effective lens position (ELP).

Third-generation formulas, such as Holladay I, Hoffer Q and SRK/T, use axial length and corneal power to predict the ELP. These formulas provide excellent refractive outcomes for most patients with normal anterior segment anatomy and a normal range of axial lengths, but they are less predictable in eyes that have more unusual anatomy.

Fourth-generation formulas incorporate more complex formulas to estimate the ELP. For example, Haigis requires measurement of the anterior chamber depth and has four “A constants” based on regression analysis. The Holladay II formula requires multiple measurements besides axial length and keratometry, including white-to-white, corneal diameter, anterior chamber depth, lens thickness, patient’s age, and preoperative refraction. Some studies suggest that these formulas are superior to third-generation formulas, especially in eyes with abnormal axial length and corneas, but data are not conclusive.¹

While third- and fourth-generation formulas are staples in the OR, the fifth-generation formulas could provide even better accuracy. For example, the Olsen formula uses ray tracing and thick lens considerations to develop a C constant to predict the ELP, which is a helpful adjunct for short eyes. Also, the Barrett Universal II formula works well for short, normal and long eyes.

Other new formulas utilize simple measurements but apply them to more complex equations, such as the radial basis functions (RBFs) from Warren Hill, MD. The RBFs utilize data interpolation and pattern recognition from the Lenstar database to create an algorithm for lens calculations, and this looks to be promising for improving accuracy. However, it will only be available on the Lenstar device. The new Hoffer H-5 equation biometric data for race and gender are meant to refine postoperative outcomes. It has been shown that men have longer eyes with flatter corneas and deeper anterior chambers, so the formulas incorporate this. Meanwhile, different ethnicities have variations in average axial lengths, so perhaps optimization should incorporate these averages. Lastly, the Ladas Super Formula makes a 3-D model using five different modern formulas to predict the refractive outcome. These formulas weren’t commercially available at the time of publication.

Unusual eyes, unusual results

Outliers in axial length measurement often result in refractive surprises. Long eyes have been a challenge and often end up hyperopic with standard calculations. We believe this is because surgeons overestimate the length of the posterior segment, thus selecting an IOL of insufficient power. Long eyes are likely to have a longer posterior segment that has a different index of refraction compared to the anterior chamber and cornea. Therefore, formulas must adjust for this.

The Wang-Koch formula for optimizing axial length fully compensates for this problem and has shown improved outcomes in long eyes with axial length greater than 25.2 mm.² These could be applied to four different IOL calculations:

• Holladay 1. Revised axial length = 0.8289 x IOLMaster AL + 4.2663.

• Haigis. Revised axial length = 0.9286 x IOLMaster AL + 1.562.

• SRK/T. Revised axial length = 0.8544 x IOLMaster AL + 3.7222.

• Hoffer Q. Revised axial length = 0.853 x IOLMaster AL + 3.5794.

Of the available formulas without optimization, the Barrett comes closest in accuracy for long eyes.^1,3

Short eyes (< 22 mm) also pose problems for accurate ELP predictions. The high IOL power and short distance to the retina can create large postoperative errors, often in a myopic direction due to anterior position of the IOL. We have not found the perfect solution for short eyes. We tend to look for a median result among the Holladay 1, Holladay 2, Barrett and Olsen formulas.

Pay attention to the posterior

When surgeons utilize only anterior measurements, refractive surprises may occur. So, astigmatism correction during cataract surgery requires accurate preoperative measurements and knowledge of the posterior cornea’s role. Although the “gold standard” has been heralded as manual keratometry, most refractive cataract surgeons use a combination of biometric and topographic values to determine the correct magnitude and axis. We advocate a minimum of three measurements, although more can be of use.

The role of the posterior cornea is critical and only studied in the last few years in eyes possessing with-the-rule (WTR) and against-the-rule (ATR) astigmatism. A large cohort found that the posterior cornea is vertically steep; this results in ATR astigmatism as the posterior cornea has negative power. When you add this to an eye that has WTR anterior astigmatism, the total astigmatism is less than predicted.⁴ The reverse is true for eyes with ATR anterior corneas — the net total astigmatism is more than predicted. In addition, the study showed that the anterior cornea marches from WTR to ATR over time in most eyes while the posterior cornea remains the same. Therefore, surgeons should avoid overtreating an eye that is WTR, since it will continue to progress towards ATR in the future.

The Baylor nomogram was designed to adjust for these measurements. The goal is to avoid undertreating ATR cases and flipping the axis on WTR cases. The nomogram shifts the threshold for selecting a toric IOL up 0.7 D, so that a toric IOL is not used until the anterior cornea has 1.7 D of WTR astigmatism. It shifts the threshold for selecting a toric IOL down 0.7 D: a toric IOL 1.5 D of toricity is used in an eye with 0.8 D of ATR astigmatism. Also, most oblique eyes are transitioning from WTR to ATR, so we tend to treat based on the anterior measurement alone.

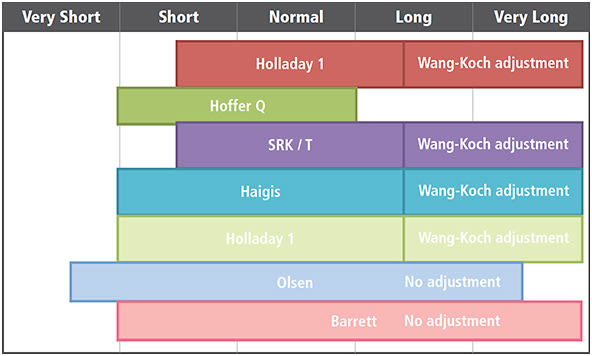
Figure. Formulas assuming normal anterior segment and keratometry.
ADAPTED FROM WARREN HILL WEBSITE

Despite the availability of the nomogram, the posterior cornea still eludes us, as it varies from patient to patient. The ideal scenario would be to measure the posterior cornea directly. Certain topographers, such as the Galilei (Ziemer), i-Optics (Cassini) and the Oculus (Pentacam), can image the posterior cornea. Although the repeatability of posterior measurements has come a long way, we still do not find it sufficiently precise to exclusively rely on it.⁵ However, it can assist when the anterior to posterior cornea measurements do not follow the standard theories. As technology improves, there may be a day when a nomogram is no longer needed.

Barrett toric calculator and Abulafia-Koch formula

Graham Barrett, MD developed the Barrett toric calculator, which internally accounts for the posterior cornea when determining the appropriate astigmatism-correcting lens. In addition, it utilizes the Barrett Universal II formula to accurately estimate ELP. Study results from the Barrett toric calculator have been promising in astigmatism correction as well as overall refractive results.^6,7 The Barrett toric calculator is now available on the ASCRS website (http://www.ascrs.org/barrett-toric-calculator) and is also built into the Lenstar LS 900.

Abulafia and Koch have developed a formula for converting anterior corneal curvature into corneal power, taking into account the posterior cornea with vector analysis.⁸ This is a nice option that allows surgeons to use their favorite formulas while incorporating the estimated contribution of the posterior cornea.

Are we there yet?

Postrefractive corneas represent a challenge in IOL calculations and can often belong to the most frustrating eyes. Measurements of the anterior surface assume a fixed anterior-to-posterior corneal curvature ratio, which is no longer valid once procedures alter the anterior corneal surface. As with toric IOL calculations, we await the availability of devices that can consistently measure posterior corneal power. Other issues include greater variability in corneal power over the central 3 mm to 4 mm and difficulty in calculating ELP (unless pre-LASIK corneal power is known).

The number of options can be overwhelming. For example, myopic eyes have more than 40 variations of formulas and measurements. The ASCRS calculator highlights established formulas, such as the Haigis-L, Masket regression and Wang-Koch-Maloney formulas. In addition, it provides new formulas and new technologies. One example is the Fourier-domain optical coherence tomography (OCT)-based IOL formula.⁹ After capturing three anterior segment OCT images from the RTVue (OptoVue), the surgeon can obtain the median net cornea power and posterior corneal power. The Barrett True K formula is also available, which does not require any historic information. These formulas can be applied to hyperopic ablations as well.

Intraoperative imaging

Intraoperative aberrometry provides a unique twist to IOL decisions. But, it will likely not make lens calculations obsolete any time in the near future, as the accuracy is not sufficiently consistent. Many factors can alter intraoperative measurements, including viscoelastic, lid speculum, ocular surface integrity, corneal edema and user error. At this time, we find it valuable as a confirmatory or complementary test rather than a way to avoid any preoperative calculations. Its use in postrefractive surgery cases and astigmatism correction are of particular interest, especially as the technology improves.

Conclusion

Patients expect precise refractive outcomes after cataract surgery, which raises the bar for how we determine IOL power. By incorporating the newest technologies and formulas, we can improve accuracy, especially for challenging eyes. Despite these advances, we must educate our patients about the possibility of unanticipated refractive ametropia — and that we have the means to address it if it occurs. OM

REFERENCES

About the Authors
	Sumitra Khandelwal, MD, is assistant professor of ophthalmology at Baylor College of Medicine, Houston, Texas, and staff ophthalmologist at Michael E. DeBakey Veterans Affairs Hospital, Houston. Contact her at SKhandel@bcm.edu.
	Douglas D. Koch, MD, is professor and Allen, Mosbacher, and Law Chair in Ophthalmology, Cullen Eye Institute, Baylor College of Medicine, Houston, Texas.
	Dr. Koch has financial relationships with Alcon, AMO, Bausch + Lomb, Carl Zeiss Meditec, i-Optics and Ziemer.