Value-Based Medicine

Decision Analysis in Cataract Surgery

By Melissa M. Brown, MD, MN, MBA

In the June column, we introduced the method of decision analysis. This methodology has its roots in economics and game theory and has been used by many sectors, including the armed services, for years. The process actually clearly points us to the most probable outcome of an intervention. What more could we want as clinicians but to know the most likely result of our treatments based on the best evidence we can gather!

The methodology is used to determine the preferred treatment option when there is a level of uncertainty. It does so by valuing all possible outcomes of an intervention. The models we use are developed with TreeAge Data 4.0 decision-analysis software; however, there are reviews of commonly used software on the Web site sponsored by the Decision Analysis Society.

The Decision Tree

Essentially, the decision tree models are a sequence of decisions and chance events over time with a probability assigned to each chance event. Each pathway through the decision tree consists of a combination of decision and chance points, or nodes, and is associated with a final path delineated at the end by a terminal node.

Each decision point is assessed with weighted values entered at the terminal nodes and the proportions of weighting entered below the branches. These data come from relevant, appropriate research such as clinical trials and quality-of-life evaluations. Data at the terminal nodes are often utilities. However, other values (dollars, $/QALY, visual acuity, decibel level, etc.) can be used depending on the topic of study. Figures 1.1 and 1.2 together are a simplified example of a decision analysis model for cataract surgery.

Figure 1.1. Illustrative Basic Decision Analysis for Cataract. The tree progresses from left to right, with increasing numbers of branches as it advances.

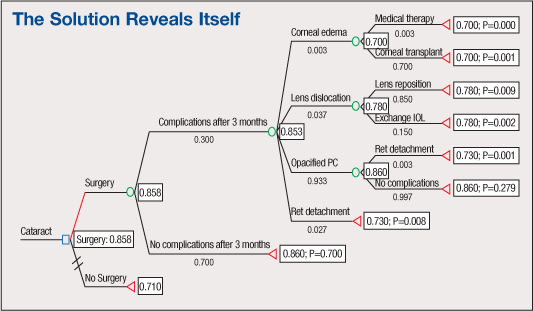
Figure 1.2. Solved Basic Decision Tree for Cataract corresponding to Figure 1.1.

The nodes in Figure 1 are represented as follows:

■ The rectangle is a decision node. The decision choice here is whether to do cataract surgery.

■ Each oval is a chance node. With each decision there is chance of incurring complications or not. The chance of each outcome is indicated under the respective branch in decimal form (decimal x 100=%). For example, with surgery there is a 70% chance to experience no complications after three months and a 30% chance of having at least one complication after three months. Of the 30% of instances where there is a complication, there is a 3% chance of corneal edema, 3.7% chance of lens dislocation, etc. Following the tree, of those who experience corneal edema there is a 70% chance of needing a corneal transplant and 30% chance of success with medical therapy.

■ Each triangle is a terminal node representing an outcome. The utilities to the right of the terminal nodes are those associated with select outcomes (1.0 is associated with full recovery with 0.0 corresponding to death).

The utilities associated with each outcome are weighted according to the chance of occurrence to derive the most probable utility outcome (seen in the rectangular boxes to right of oval decision nodes) for each major branching from the decision node. In our models, we use the average case for utility determination.

In the illustrative case above, the preferred strategy is surgery with a utility of 0.858 compared with no surgery and a utility of 0.710. The total QALY gain can be determined by multiplying the utility gained (i.e., 0.858) by the number of years the benefit is likely to last. In this case, a 20-year life expectancy following cataract surgery would yield 17.16 QALYs.

Don't get too bogged down in these details. The essentials are that decision analysis:

► demonstrates the preferred strategy under uncertain circumstances
► allows for decisions to be made using information that is relevant to our patients — their desirability of various outcomes
► determines expected gains in quality-of-life related to a therapy and compares them with other therapies or to no therapy

Achieving Objectivity

This limited discussion on decision analysis is attempted in the hope that we can begin to appreciate that subjective assessments can be made objective and that it is most important that physicians seek to understand and manage what medical evidence is used to establish overall treatment criteria. Most importantly, the methodology utilizes the opinions of the folks for whom we wish to enhance the quality of their lives through thoughtful medical interventions. OM

Melissa M. Brown, MD, MN, MBA, is president and CEO of the Center for Value-Based Medicine in Philadelphia. She can be reached via e-mail at mbrown@valuebasedmedicine.com.