Post-Multifocal IOL Wavefronts: Are They Reliable?
Physical testing with a fluid-filled eye provides guidance.

BY CHARLES CAMPBELL

Many patients who have undergone cataract surgery and subsequent IOL implantation are left with some residual refractive error. In this age of highly successful refractive surgery, it is natural to consider removing residual refractive error using a wavefront-guided laser refractive treatment. However, when the implanted lens is a multifocal IOL, are wavefront measurements still useful for planning a refractive surgical treatment?
To address this question in a more rapid and controlled fashion than would be possible in a clinical trial, a two-part study has been performed consisting first of a theoretical treatment followed by physical testing. The theoretical treatment was done to predict the result of measuring an eye with a wavefront refractor. A physical test using a special fluid-filled test eye allowed the IOL to act optically just as it would in a human eye and permitted it to be measured with a commercial wavefront eye refractor. The results were then compared to theoretical predictions.
In this article, I will describe my findings and present my opinions on the reliability of and potential applications for wavefront measurements obtained from eyes implanted with multifocal IOLs.
Theoretical Treatment
A Shack-Hartmann wavefront sensor divides the wavefront under examination into small square areas through the use of an array of lenslets. Each of these lenslets is a powerful positive lens concentrating light from the portion of the wavefront through which it passes onto a charged coupled device (CCD) sensor. The position of this concentrated spot of light on the sensor is used to find the slope of the wavefront portion passing through the lenslet. The ensemble of slopes from each lenslet in the array is then used to reconstruct the wavefront. Thus, a critical part of the Shack- Hartmann wavefront-sensing method is the character of the concentrated spot of light, the position of which provides the necessary wavefront slope information. Normally, a small area of a wavefront does not depart in a significant manner from a small toric surface that is tipped with respect to the optical axis of the instrument. But in the case of a diffractive bifocal IOL it is quite possible that one of the echelet edges, where the wavefront abruptly jumps by approximately one-half of a wavelength, will pass through a lenslet. A straightforward calculation using diffraction optics principles predicts that when a halfwave phase jump occurs near the center of a lenslet, the light concentrated on the sensor splits in two — so two spots should be formed instead of one. This doubling is also predicted to occur if more than one echelet edge passes through a single lenslet. In addition, if the phase jump is somewhat less than one-half a wavelength, one of the two spot will be brighter than the other. This typically occurs because a diffractive bifocal IOL is designed to have onehalf wavelength phase jumps at a mid-visible wavelength of 555 nm, whereas wavefront refractors measure using infrared radiation in the range of 760 nm to 850 nm. So, how will a given wavefront eye refractor deal with doubled spots and what will the displayed measurement show? Some multifocal IOLs do not use a diffractive design but use a multizone refractive design where the power of the lens varies from one annular zone to its neighbors on both sides. While there are no abrupt wavefront phase jumps in these designs, the wavefront can exhibit significantly high local curvature in the transition zone between the main annular power zones, so that some lenslets will sample quite

irregular portions of the wavefront. In addition, the local power and hence, wavefront slope, is expected to vary markedly over fairly short distances. So while the wavefront sensor will not have to deal with doubled but well-defined spots, it will have to deal with a wavefront that will appear to be highly aberrated in an overall sense.
Experimental Methods
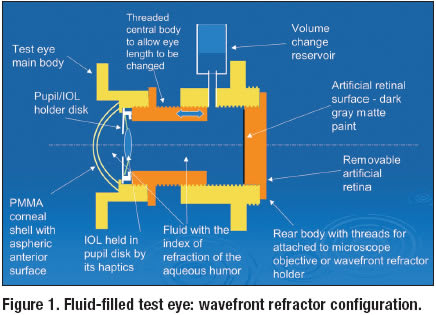
To physically test the performance of a Shack-Hartmann wavefront eye refractor when measuring an eye implanted with a multifocal IOL, we used a special test eye designed to accurately simulate the optical conditions found in a human eye (Figures 1 and 2).
The only optical element, other than the IOL itself, in a human eye with an IOL implanted, is the cornea, a highly curved meniscus shell with central thickness of approximately 0.5 mm. A representative average human cornea has a central radius of curvature of 7.8 mm and is aspherical with a conic constant of -0.2. The average cornea has a posterior radius of curvature of 6.4 mm with a conic constant of -0.4. To duplicate the optical performance of this average cornea, the test eye was built with a PMMA meniscus shell as its first element. The central anterior radius of curvature of the shell in the test eye was 7.8 mm. The surface was cut as an ellipse of revolution with a conic constant of -0.1. The central thickness of the shell was 0.5 mm.
The posterior surface was spherical with a radius of curvature of 7.22 mm. These parameters were chosen because when a collimated beam of light enters such a shell and exits into fluid with the index of refraction of a aqueous humor of the eye (1.336), the wavefront has the same central vergence and the same higher order aberration (HOA) as does a similar wavefront exiting the average cornea into the anterior chamber of the eye. Thus, if the IOL is held with respect to the artificial cornea at the same distance as it is held from the cornea in the human eye, the same optical condition exits for both situations. In the test eye, the artificial corneal shell is attached to the main body of the eye and the inside of the test eye is filled with fluid. To provide a fluid with the correct index of refraction, sucrose was added to water to create a 2.1% solution. The IOL was held in a specially made disk within the test eye, which allowed the lens to be wholly supported by its haptics, thus suspending the IOL identically to how it is supported in the human eye. The disk in the test eye had a central clear aperture that simulated the pupil created by the iris in the human eye. This disk was held within the body of the eye at a distance of 3.5 mm from the posterior surface of the corneal shell so that the IOL was held at the same distance from that surface as it is held from the posterior corneal surface in the human eye. This is an important detail, because if the lens is incorrectly spaced, the blurring effect of imaging objects at various viewing distances will not be similar to that found in the human eye.

The final element in the test eye was an artificial retinal surface, which was the inner flat surface of the plug that screwed into and sealed the rear of the test eye. This surface was painted with a flat dark gray paint that has been found to backscatter light with the same intensity as a human retina when irradiated with near infrared radiation. This allows a wavefront eye refractor to successfully measure the refractive state of the test eye just as it would measure the refractive state of a human eye. The rear plug of the test eye was designed to be replaced with a transparent window constructed of 1-mm–thick microscope slide, whose internal surface was at exactly the same axial position as the artificial retinal surface. The test eye was used in this configuration to adjust its overall length to achieve the desired distance refractive error via the use of special optical apparatus. For these tests, the distance refractive error of the test eye was adjusted to 0.0 D, i.e., an object at optical infinity. The special optical apparatus consisted of a Badal optometer illumination system having a 100-mm focal

length optometer lens and a 10 μm pinhole source irradiated with a halogen lamp, a 10 X microscope objective focused on the inner surface of the rear window of the test eye, a CCD camera (pixel size 5.4 x 5.4 μm) attached to the microscope objective and a computer to display the live image created. The Badal optometer was set to produce collimated light (0.0 D vergence) and the length of the test adjusted until the best point spread was created as viewed by the microscope system. The vergence was then changed to simulate viewing a near object until a second good point spread appeared. This latter step was taken to insure that the near focus of the multifocal IOL was not mistaken for the distance focus. With the test eye properly adjusted for length, the transmission window was replaced with the artificial retinal plug and the test was measured with a wavefront eye refractor just as a human eye would be measured.
Results
The test eye was first measured with no IOL in place to assess the amount of HOA induced by the corneal shell alone. It was found that the coefficient of the Zernike term Z0 4 had a value of 0.20 μm. No other HOAs were found to be significant. A number of multifocal IOLs, both diffractive and refractive, were then tested. As the general results were similar for a given type, only the results of one of each type are given here. The diffractive lens reported was a +25 D bifocal lens model ZM900 (Tecnis, AMO [Advanced Medical Optics], Santa Ana, Calif.). This lens is designed to remove 0.27 μm RMS spherical aberration error in addition to having a 4.0 D near point add. The WaveScan system (AMO/VISX) found a residual sphere and cylinder +0.13 DS, -0.08 DC x 160. This is, within experimental uncertainty, the vergence that the test eye was set for. The only significant HOA found for coma (Z1 3 and Z3 -1) where the magnitude was 0.096 μm and for spherical aberration (Z04 ) where the magnitude was -0.097 μm. Note that the IOL is designed to remove 0.27 μm and it is known that the corneal shell alone contributed 0.20 μm. Thus, the measured value is within 0.03 μm of the expected value. The coma found was most probably caused by a slight decentration of the lens with respect to the artificial pupil and corneal shell. Examination of the image of Shack-Hartmann spots revealed doubled spots of unequal intensity. When the instrument was decentered with respect to the test eye by one-half a lenslet period (0.2 mm), it was found that some of the doubled spots resolved into a single spot as was expected as the half wave phase jump was moved out of the central portion of the associated lenslet (Figure 3). The refractive lens reported was a +25 D multifocal lens model NXG1 (ReZoom, AMO). This lens is designed to have a near point add of 4 D. The WaveScan system found a residual sphere and cylinder -1.27 DS, -0.07 DC x 166. This value is quite different from the 0.0 DS to which the test was set. The coefficients of the higher order aberrations reported were quite different from zero and are given in magnitude axis form in the Table, shown below. Figure 4 shows the spot patterns for the refractive multifocal IOL.

Summary
Measurements of the diffractive bifocal lens yielded results that were sufficiently close to the expected results that they would have been reasonable to use as a basis for a refractive treatment to remove residual refractive error. The residual sphere and cylinder error was that set into the test eye using the optical rail apparatus. The residual higher- order error was in accordance with the known aberration induced by the corneal shell that the corrective effect of the diffractive bifocal IOL.

Measurement of the refractive multifocal lens yielded results that were not representative of the setting of the test eye with the IOL in place. There was little, if any, primary spherical aberration found but a significant amount of secondary spherical aberration. In all likelihood, if these wavefront findings had been used to create a treatment, the multifocal effect of the IOL would have been erased by an opposite acting aspherical correction. It is unclear where the mean spherical error of the eye would have ended, although it would have most likely have been returned to emmetropia. It is my opinion that surgeons should use caution when using wavefront findings taken on eyes that have multifocal IOLs in planning postoperative refractive corrections. Wavefront measurements taken on eyes with diffractive bifocal intraocular lenses implanted appear to give results that can be used to plan further treatments, but wavefront measurements taken on eyes that have refractive IOL implanted should not be used. In all cases, subjective refraction results should be compared to wavefront eye refractor results to insure that the wavefront findings are useful.

Charles Campbell is a consultant in the field of ophthalmic optics. He has worked in this field for 31 years specializing in the areas of ophthalmic instrument design, refractive error of the eye, corneal topography and ophthalmic lens measurement. This work was done in his role as a consultant for AMO/VISX. He can be e-mailed at ceccec@pacbell.net.