REFRACTIVE SURGERY CHALLENGES, PART 2 OF 3
Zernike or Fourier: Does it Matter?
Two experts bring you up to speed on the differences and discuss the effect on outcomes.
BY STEPHEN BRINT, M.D., AND JOHN VUKICH, M.D.

The advent of Fourier analysis as an alternative to Zernike polynomials for characterizing the optical wavefront raises the question of whether the newer method should replace the standard in all refractive surgery platforms. Advocates for Zernike polynomials maintain that this approach is best-suited for our current treatment technologies, providing the necessary accuracy without introducing artifacts or being overly sensitive to noise in the measurement and subsequent treatment. Advocates of Fourier analysis say it provides a more detailed interpretation of the wavefront, which is especially important for treating highly aberrated eyes and eyes with aberrations induced by previous treatment.

Although it's too early to tell whether one of these, or perhaps some other method, will become dominant, the merits of both will certainly be evaluated further. Each will likely evolve, along with all of the other elements of wavefront-guided refractive surgery, leading to continued improvement in patient outcomes.

In this article, Stephen Brint, M.D., associate clinical professor at Tulane University School of Medicine, and John Vukich, M.D., medical director at the Davis Duehr Dean Center for Refractive Surgery and assistant clinical professor at the University of Wisconsin, discuss some of the frequently asked questions about Zernike polynomials and Fourier analysis, and how the differences between them affect or don't affect clinical outcomes.

The use of an increasing number of Fourier sine waves and Zernike polynomials to describe a complex shape demonstrates a corresponding improvement in resolution and shape. With the Zernike reconstruction, there is a significant smoothing of details. Image courtesy of John Vukich, M.D.

How does the accuracy of Fourier analysis compare with the accuracy of Zernike polynomials?

Dr. Brint: The accuracy of Fourier analysis and Zernike polynomials is rather difficult to compare because the order of the Zernike polynomial and the number of points included in the Fourier analysis will both affect accuracy. In addition, the accuracy of a mathematical function based on observed data may be "pinpointed," but if the data are not accurate then this provides no benefit. (In fact, it is a potential drawback.) The accuracy of any analytical tool should be appropriate to the accuracy of the data being analyzed. With specific reference to wavefront-guided refractive surgery, the accuracy of the wavefront analysis should also be appropriate to the ability of the laser to treat the generated wavefront.

A sufficiently high-order Zernike polynomial would be indistinguishable from Fourier synthesis. With both, an infinite series of increasingly complex terms would perfectly fit any series of data points. VISX suggests that its Fourier synthesis is roughly equivalent to a 20th-order Zernike polynomial. Alcon has no evidence that a Zernike fit past the eighth order provides any material benefit to a patient, nor can any Zernike fit past the eighth order be treated with current laser technology. (Huang DH. Physics of customized cornea ablation. In: Krueger, RR, et al., eds. Wavefront Customized Visual Correction: the Request for Supervision II. Thorofare, NJ: SLACK Incorporated; 2004: pp 171-180.)

Accuracy in the context of wavefront-guided surgery should not be evaluated on the basis of "how accurately can I fit a large number of somewhat-variable data points," but instead "how accurately do I need to be able to determine the wavefront in order to appropriately treat a patient?"

Dr. Vukich: It is important to note that both Zernike and Fourier methods are interpreting the same Hartmann-Shack data. The differences between the methods do not affect their accuracy as much as their resolution. The fundamental shape remains the same from the input data, but the resolution of the contour and the detail that is available to bring into the shape is greater with the Fourier method.

A graphic demonstration of this can be seen with the interpretation of a test object, such as the contour of a human face in profile. (See image on page 33.) The use of an increasing number of Fourier sine waves and Zernike polynomials to describe a complex shape demonstrates a corresponding improvement in resolution of the shape. However, it is evident that compared with Fourier analysis, even when using up to 10 orders of Zernike polynomials, there is a significant smoothing of the detail with Zernike polynomials.

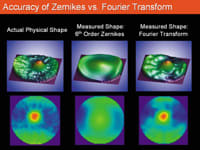
An actual physical test shape as described by sixth-order Zernikes and Fourier analysis (See "Accuracy of Zernikes vs. Fourier Transform," on page 34.), provides further evidence of the smoothing effect inherent in Zernike analysis. The Zernike solution demonstrates a close resemblance to the test shape, but has a noticeable loss of detail. The Fourier transformation provides an increased level of detail and shows a greater resemblance to the initial shape.

Using Zernike polynomials to interpret Hartmann-Shack data is analogous to using a standard television to watch a high-definition broadcast. Even though the information is present to create a high-quality picture, the image is viewed at a lower resolution than what is potentially available.

	A test shape as described by sixth-order Zernikes and Fourier analysis. Image courtesy of John Vukich, M.D.

Are Zernike polynomials sufficiently accurate to characterize abnormal optical wavefronts?

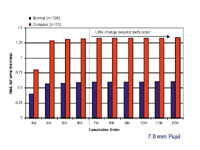
Dr. Brint: Evidence to date suggests that Zernike polynomials of a moderate order are sufficient to accurately characterize abnormal optical wavefronts. In a study conducted with the Alcon LADARWave system, Zernike polynomials of increasingly higher order were fit to the Shack-Hartmann images from a series of normal and highly aberrated eyes. (See graph below for results.)

As can be seen, the ability of the Zernike polynomial to accurately capture the wavefront shape significantly increases between the third to sixth orders (i.e., the measured wavefront error is steadily increasing). This is a reflection of an increasingly more accurate fit. However, past the sixth order there is little or no change in the measured wavefront error from either the normal or complex eyes. This suggests that there is little incremental benefit to fitting the wavefront to higher than sixth or eighth order.

In short, there is no evidence to suggest that Zernike polynomials of sixth to eighth order cannot accurately characterize abnormal optical wavefronts. However, as discussed elsewhere in this article, there are considerable potential negative effects to "over fitting" by using a technique such as Fourier analysis.

Dr. Vukich: Abnormal optical wavefronts from either induced aberrations from prior surgery or from corneal pathology remain a challenge in custom correction.

The Zernike polynomial solution has been demonstrated to be inadequate in cases of keratoconus and penetrating keratoplasty. Michael Smolek and Stephen Klyce have reported that when Zernikes are used to fit a complex surface, such as a keratoconic cornea, there is a substantial amount of fit error. (Smolek MK, Klyce SD. Zernike polynomials are inadequate to represent higher order aberrations in the eye. Invest Ophthalmol Vis Sci. 2003;44:4676-81.) Zernikes, if limited to the sixth order, may not be fully adequate to describe complex wavefront patterns in refractive surgery. As such, the resolution of the Zernike interpretations up to the sixth order provides an inadequate picture of patients with corneal pathology and abnormal wavefronts. There is no argument that Fourier transformation yields greater detail than sixth-order Zernike polynomials. Whether or not this will allow us to provide therapeutic custom treatment remains to be proven. Logically, we would anticipate that a better quality image would be an important step in providing a better quality of treatment.

RMS wavefront error calculated from Zernike polynomials of increasing order. Image courtesy of Stephen Brint, M.D.

Is Fourier analysis too sensitive for the types of eyes seen in everyday practice?

Dr. Brint: This question of being "too sensitive" is one that is often raised with Fourier analysis. Certainly there is a concern because of the much greater sensitivity of Fourier analysis to anomalous data points in the Shack-Hartmann image.

In essence, the Fourier method presumes that the data from all lenslets are equally reliable, something that is highly unlikely. There is no way to "weight" data points or to evaluate and/or discard highly suspect points. For evaluating optical systems that are invariant (e.g., fixed telescopes, lenses), Fourier analysis would likely be as useful as Zernike analysis for characterizing the optical wavefront. However, with a live eye the effects of the tear film, accommodation, and fixation are all known to produce some variability in the Shack-Hartmann image. As such, adopting a mathematical analytical system such as Fourier, which presumes a perfect and repeatable image, seems counterintuitive. A Fourier analysis would presume that image 2a and 2b (See images below.) were equally reliable for analysis purposes. A Zernike analysis would limit the negative effects of the tear film distortion evident in image 2b.

It is not possible to definitively state that Fourier analysis is too sensitive for normal eyes. However, it can be stated that the potential to mischaracterize normal optical wavefronts from the human eye with Fourier analysis is higher than for Zernike analysis, primarily as a function of the normal variability in the Shack-Hartmann image.

Dr. Vukich: An enhanced level of detail in the analysis of the optical wavefront of all eyes is a desirable goal. There is a continuum in the amount of aberration seen in a normal population. Unfortunately there is not a bright line that divides what we can consider normal from abnormal. All of the available custom lasers have demonstrated enhanced clinical outcomes using Zernike wavefront analysis compared to their standard ablation profiles. What has also been common to all custom laser platforms is the challenge of providing effective therapeutic treatments in abnormal or highly aberrated eyes. If we are going to limit our treatments to only those patients with spherical myopia perhaps an argument can be made that increased resolution of the wavefront is unnecessary. The fact is that in a clinical practice we can expect to see a broad range of optical aberrations. The ability to detect a more detailed characterization of the wavefront is an important step in understanding and eventually realizing the full potential of custom ablation. There is no reason to believe or data to support that increased resolution of wavefront detail could adversely affect treatments. Fourier analysis has been incorporated as the exclusive method for all normal treatments on the VISX wavefront-guided refractive surgery platform using the upgraded version 3.54 software. This upgrade has been reviewed and approved by the FDA. It has been demonstrated to be, at a minimum, functionally equivalent to the previous generation of custom ablations. Importantly, Fourier analysis also offers the potential to characterize more complicated wavefronts.

	Shack-Hartmann image quality. Fourier treats these as equally reliable; Zernike limits the effects of tear film breakup in image 2b. Image courtesy of Stephen Brint, M.D.

Is it desirable to use high-resolution images of the optical wavefront for custom ablation? Why or why not?

Dr. Brint: High-resolution images of the optical wavefront are always desirable, whether for custom ablation or diagnostic purposes; the key is defining resolution. The resolution required for appropriate wavefront-guided surgery is the resolution possible from the mechanical imaging system, and limited by the characteristics of the human eye. The first is related to the data collected, and the second is related to interpreting those data.

Current Shack-Hartmann detectors typically have several hundred data points to analyze in the image they capture; the number of points is limited by both optical considerations and such things as "point crossover" effects. In the case of the LADARWave, the Zernike polynomial is a best-fit regression to these several hundred data points. More data points improve the reliability of the fit, as individual anomalous points become less important. Higher resolution imaging would further improve any Zernike fit, increasing the reliability of higher-order Zernike terms. Some industry competitors in early literature suggested they didn't use all data points in determination of their Zernike polynomial, which would certainly weaken any subsequent wavefront calculation.

Fourier analysis calculates the wavefront on the basis of each data point collected. More data points increases the complexity of the Fourier equation, with potentially no improvement in the characterization of the wavefront relative to the needs of the patient.

In the Zernike, more data points are always useful, even if there is some "noise." The interpretation of the data is really determined by the order of the Zernike polynomial. This allows for appropriate specification of the ablation pattern on the basis of "filtering out" artifacts, such as transient tear film effects. This inability to filter is a weakness of the Fourier method; it is constrained by use and fit to all available data points, needlessly incorporating measurement noise. Filtering data with the Fourier method is too complex to be practical.

Dr. Vukich: To provide a custom treatment, all of the elements of the treatment need to be at the same level of resolution. In other words, the capture and interpretation of the information, the registration and centration, tracking of the delivery, and the actual ability to deliver are necessary to provide a high-quality outcome. Therefore, it is not incumbent upon simply the resolution of the wavefront. Instead, it is the ability to translate that exact shape onto the exact location of the cornea in a way that is both reliable and reproducible. To that extent, improved tracking, improved autocentration, and torsional registration, which have been upgrades in the latest generation of lasers, enable us to use these high-resolution images in a way that translates their effect into a better quality outcome. Without those additional features an approximation, or less precise image, may allow greater latitude for error in the delivery process. The soft edges that a Zernike interpretation adds to the wavefront is more forgiving of angular or rotational misalignment, but ultimately will limit the accuracy of the custom treatment.

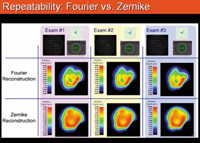
Three Hartmann-Shack exams of the same eye were taken over a 15-minute period. For each exam, the target ablation pattern was calculated using Zernike polynomials and Fourier reconstruction. The increased complexity of the Fourier-derived shape is consistent and reproducible at each of the exams. Image courtesy of John Vukich, M.D.

Is it optimal to treat as high an order of aberration as possible? Why or why not?

Dr. Brint: The first concern is whether or not it is possible to treat higher-order aberrations. Evidence from Alcon's CustomCornea (Zernike-based) FDA clinical trials showed that appropriate treatment of higher-order aberrations can produce an improvement in the optical quality of the eye. However, no such data were reported for the VISX CustomVue system, which was also Zernike-based. This suggests that the method of analyzing the wavefront is not the limiting factor. Other factors, such as appropriate registration of the wavefront to the eye and autofogging to compensate for accommodative effects (both present in the Alcon LADARWave device, though not in the VISX Wavescan) appear at least as important as the method of wavefront analysis. To date, it remains to be seen whether a move from Zernike to Fourier analysis will show any demonstrable improvement over CustomVue results.

As to the correcting of higher-order aberrations, it appears intuitively obvious that the best quality optical image at the retinal plane will provide the best possible vision for each patient. However, we know that there is a diminishing return. Correcting sphere and cylinder appropriately provides considerable benefit to the patient. With each higher order of Zernike correction there tends to be modest incremental improvements.

There are known measurement errors with any Shack-Hartmann system. At some high Zernike order the polynomial may be fitting the measurement errors rather than the aberrations of the eye; it would not be in the patient's best interest to treat these. In the case of the Zernike polynomial, the order can be appropriately chosen to limit this effect. There is no such option with the Fourier system; all noise and errors in the Shack-Hartmann image will be included in the Fourier equation.

The current goals in treating higher-order aberrations are first to appropriately compensate for aberrations induced by the surgery, and second to reduce preoperative higher-order aberrations. As the accuracy with which we can achieve this goal improves, clinical data will point us to the next level of refinement in wavefront-guided correction. It may be that there are optimal aberrations for the human eye, or for each individual. Current data may provide the direction to further customize custom surgery.

Dr. Vukich: First, it is important to remember that the term "orders of aberrations" refers to the Zernike interpretation. They only have relevance in terms of how a wavefront is decomposed into a polynomial expression. This is one of the confusing aspects of speaking of Fourier analysis vs. Zernike interpretation. Fourier analysis is an image of the wavefront. The Zernike orders represent how many polynomials are used to extract that information from the wavefront. Therefore, the Fourier image provides a high-resolution interpretation of the wavefront in which you really can't speak of orders.

However, the equivalent results of Fourier and Zernike can be compared. When this is done it would require a 20th-order Zernike interpretation to provide an image that appears to be of the same quality as provided by Fourier. While it is not relevant to talk about orders in Fourier, a rough equivalency can be made in terms of the quality of the image provided.

It would seem intuitive that the greater the accuracy of the wavefront interpretation, the better the ability there is to correct the aberrations that are in the visual system. To what extent this will result in better quality of vision will depend in part on how much aberration is present in the first place. For an eye that has minimal higher-order aberrations, the improved quality of a Fourier image probably will not be as critical as in a patient who has significant aberrations in his or her visual system.

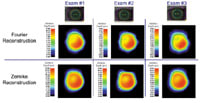
Three Hartmann-Shack exams of the same eye captured on three consecutive days. For each exam, the target ablation pattern was calculated using Zernike polynomials and Fourier reconstruction. The similarity of the target ablation profile at each of the exams demonstrates that transient variables such as tear film effects do not significantly alter the calculated treatment. Image courtesy of John Vukich, M.D.

Can tear film be problematic for either approach and how might each approach compensate for that?

Dr. Brint: This question returns to the fundamental principles of Shack-Hartmann technology. The tear film is a critical component of the eye's optical system; disruption of the tear film will compromise the quality of the image captured by the aberrometer. Whether Fourier or Zernike, the mathematical modeling of the wavefront depends on access to an accurate Shack-Hartmann image to process. This being stated, the aberrometer should be designed to mitigate the effects of tear film disruption.

One of the easiest and most effective means of reducing errors related to the tear film is to take advantage of the transient nature of most tear film disruptions. If a tear breakup occurs, a system designed to take several images in quick succession will have all of them compromised. A system set up to delay the capture of individual images, such as the LADARWave, will not be subject to this limitation. At least one blink is likely to occur between successive image captures. With this process, the effects of the tear film disruption on one Shack-Hartmann image are not repeated on subsequent images. The differences between images make it easy to determine which image points have been subject to transient effects and which have not.

While appropriate system design may limit the effects of tear film variability on the Shack-Hartmann image, it is also important that any such effects have a minimal impact on the calculated wavefront.

By nature, the Zernike polynomial series attempts to characterize the wavefront as a complex best-fit surface. One or two anomalous data points will be weighed against the several hundred more reliable points. This is much like a single anomalous refractive outcome, which does not materially affect one's "attempted vs. achieved" nomogram plots.

On the other hand, the Fourier polynomial considers each data point and includes them all in the wavefront surface. Each point, even those that may be compromised by a poor tear film, will therefore have a measurable effect on the generated wavefront.

In general, tear film disruptions (or other effects that reduce the Shack-Hartmann image quality) will affect both Fourier and Zernike polynomials, but the Fourier analysis will be more sensitive to such effects. The LADARWave Zernike-based system is evidently robust to tear film effects, based on achieving improved optical quality in the FDA trials. It remains to be seen what clinical outcomes will be achieved with a Fourier-based system.

Dr. Vukich: Tear film is the first refractive surface on the eye and it is an important component of the quality of the corneal surface. It influences the quality of the Hartmann-Shack data and it also influences the quality of the optical image and the wavefront that is generated through this surface. The Hartmann-Shack centroids are generated by averaging multiple images over a very short period of time, mitigating the effect of tear break up. A minimum of three composite images are generated and checked for quality and consistency. Once the quality of the raw data is confirmed, Fourier analysis is used to generate a characterization of the optical wavefront.

If the effects of tear film are not adequately controlled, in theory we might expect a more detailed analysis to demonstrate variability over multiple exams. In clinical practice this has not been the case. The consistency of the Fourier analysis can be demonstrated by capturing the wavefront of a single eye at 3-minute intervals. (See "Repeatability: Fourier vs. Zernike," on page 40.) For this example the same Hartmann-Shack data was reconstructed using the Fourier method and the Zernike method. On three different exams, the resulting wavefront maps were translated into an ablation target map. It is evident that both the Fourier and Zernike reconstructions are repeatable. The increased complexity of the Fourier-derived shape is consistent and reproducible. The size, orientation, and shape of these aberrations is very similar from one exam to the next, indicating that the features are not influenced by measurement, noise, or fluctuations in tear film. Furthermore, each of the Zernike-based target maps show the smoothing effect of Zernike reconstruction.

A repeatability analysis of a different eye, this time taken over three consecutive days demonstrates that wavefronts generated by Fourier analysis are consistent on a day-to-day basis. The images above show an example of the same eye of the same patient captured on three consecutive days. This demonstrates that wavefronts are repeatable not only over a period of minutes, but also on a day-to-day basis. In theory, tear film quality should be a consideration for both Zernike and Fourier. In practice, repeatability studies have demonstrated that this has not been a clinical issue.

Closing Thoughts

Dr. Brint: The whole question of Fourier vs. Zernike is in some sense a nonissue to surgeons today; the mathematical algorithm for describing the wavefront is at this point NOT a limiting factor with regard to wavefront-guided ablations. There are considerably more important factors affecting the success of custom ablation. Some factors are manageable today, such as appropriate wavefront registration and compensation for accommodative effects and the use appropriate ablation registration with a flying small-spot Gaussian beam. Some other factors, like the biomechanical and corneal healing responses of the patient, remain to be definitively resolved. The latter factors are the issues whose solution will truly raise the bar with respect to wavefront-guided laser correction. The suggestion that Fourier analysis is "beyond Zernike" is not only suspect, but also does nothing to advance the state of the art in wavefront-guided refractive surgery.

Dr. Vukich: The importance of how the wavefront is interpreted, such as by using Zernike or Fourier algorithms, is only one component of the entire custom ablation system. Each individual component needs to be optimized in order to provide the next level of treatment and outcome. The change to Fourier transformation and interpretation of the wavefront represents one step in the process.

Fourier is indisputably a higher-resolution image of the wavefront and a more accurate interpretation of the visual aberration in the human optical system. This information can only help in the customized treatment of refractive errors and ultimately, combined with improved delivery systems, it will hold the key to treating not only normal eyes, but eyes that have had induced aberrations from surgical complications or progression of natural pathology.

Dr. Stephen Brint is associate clinical professor at Tulane University School of Medicine in New Orleans, La. Dr. John Vukich is medical director at the Davis Duehr Dean Center for Refractive Surgery and is assistant clinical professor at University of Wisconsin, in Madison, Wis.

Dr. Brint has no financial interest in the information contained in this article. Dr. Vukich is a consultant to VISX Inc.

In the next installment of Refractive Surgery Challenges: Where epi-LASIK fits in