Advertisement

PentaVision

Ophthalmology Management

Article

Using Wavefront Today

Even without a laser, it's a remarkable tool. Here's how to take advantage of it now.

By: Christopher Kent, Senior
Ophthalmology Management September 1, 2002

Using Wavefront Today
Even without a laser, it's a remarkable tool. Here's how to take advantage of it now.
By Christopher Kent, Senior Associate Editor

Bright and early Saturday morning at this year's ASCRS meeting in Philadelphia, five surgeons spoke about their experiences using wavefront technology, with the emphasis on how to use this technology before the eventual FDA approval of customized ablation. Here, we'd like to share some of the highlights of that presentation.

Demystifying "irregular astigmatism"

David. R. Hardten, M.D., pointed out that many tools can measure a patient's refractive error in terms of sphere and cylinder, but they don't allow you to classify those irregularities, diagnose them, or follow them over time. In contrast, wavefront testing goes beyond defining the familiar spherical and cylindrical portion of a patient's refraction and provides detailed information about higher-order aberrations.

Any measuring tool that breaks new ground is bound to have a number of uses. Dr. Hardten spoke about four ways in which his practice currently uses wavefront technology.

Because this patient has almost 30% higher-order aberrations, waiting for custom ablation is worth considering.

Screening refractive surgery patients

Dr. Hardten explained that he currently uses wavefront data in much the same way as standard refraction data. However, knowing how much of a person's refractive error is made up of higher-order aberrations can make it possible to more realistically weigh the value of postponing refractive surgery or switching to alternatives other than LASIK.

For example, if wavefront data show that the patient's higher-order aberrations are less than 20% of the total aberrations in the eye, and the patient is happy with the way he sees in spectacles, Dr. Hardten treats the patient using currently approved technology. If the patient's higher-order aberrations account for more than 20% of total aberrations, he encourages the patient to wait for customized ablation. Twenty percent is a significant amount, and customized ablation may make it possible to treat both things at once.

At the same time, a patient with a fairly large refractive error, say -8D, is probably a good candidate for simply eliminating sphere and cylinder regardless of the amount of higher-order aberration. The dramatic difference in vision that will result (and the relatively low percentage of higher-order aberrations when compared with sphere and cylinder) will probably produce a happy post-LASIK patient. If you increase higher-order aberrations unintentionally during the procedure and this causes symptoms, Dr. Hardten points out, you can go back and treat them later.

Dr. Hardten offered two examples:

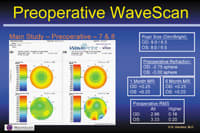
Thirty percent higher-order aberrations. An individual came in off the street to inquire about refractive surgery. He was about 20/40 uncorrected OS, with a -1.0D sphere, best-corrected to 20/20 on a manifest refraction. The "wavefront refraction," was -0.83, -0.21. In the pre-op wavefront maps (shown below) the overall aberration map (top) shows a typical myopic pattern, kind of a bowl shape with cooler colors in the middle.

Dr. Hardten subtracted out the -0.83 and -0.21 factors to show the higher-order aberrations; the resulting map (bottom) showed that this patient has a significant amount of coma, and that almost 30% of his visual problem consists of higher-order aberrations.

In this situation, Dr. Hardten told the patient: "If we do your correction with current day technology, assuming we don't induce any aberration or correct any aberration other than the planned correction, we're going to correct about 70% of your problem. We will, at best, make you see as well as you see in your glasses currently, but we can't make you see any better than that."

Patients like this may choose to wait for customized ablation before having refractive surgery. (Of course, a patient with the same amount of aberration but a refraction of -10D would have a much smaller overall percentage of higher-order aberration, making it more likely that he'd be satisfied with current laser vision correction.)

This patient has less than 10% higher-order aberrations, making him a good cadidate for conventional refractive surgery.

Ten percent higher-order aberrations. This patient's preoperative manifest refraction was ­2.75D in one eye, and ­3.00D in the other eye. Preoperative topography found a little bit of asymmetrical astigmatism, which showed up as aberration on the wavefront mapping, along with the typical myopic pattern. (See image, below.)

Here the total root mean square (RMS) value preoperatively, including lower-order aberrations, was 2.96 in the right eye and 3.33 in the left eye. (For an explanation of RMS, see "A Brief Glossary of Wavefront Terminology".) But when Dr. Hardten subtracted out all of the lower-order aberrations, the right eye had a higher-order RMS of 0.18. The left eye had a similar amount of higher order aberration. This meant that higher-order aberrations accounted for a little less than 10% of the total aberrations in this patient's vision.

Under these conditions, Dr. Hardten advised the patient that standard (nonwavefront-guided) refractive surgery was probably a good option, and he proceeded. The post-op measurements still showed some residual coma in the right eye, and post-op point spread function showed the same thing. However, the surgery reduced the overall RMS in both eyes, with only a minimal increase in higher-order aberrations (from 0.18 and 0.20 to 0.24), and the patient's post-op vision was very good -- 20/20 uncorrected, + 0.5D sphere in both eyes.

Other practical uses for wavefront

Dr. Hardten's practice also uses wavefront technology to serve several other purposes:

Combining wavefront readings with other types of measurement. If a patient's wavefront readings show a lot of aberration but corneal topography is normal, that means the distortion is somewhere else inside the patient's visual system -- probably in the lens. This suggests that the patient may benefit more from cataract extraction or lens extraction than from refractive surgery on the cornea.

Conversely, if the wavefront shows a lot of higher-order aberrations and the topography also shows this, the patient is probably a good candidate for customized treatment.

Following cataract symptoms over time. Dr. Hardten pointed out that as the symptoms of cataract development worsen over time, corneal topography will remain unchanged, but wavefront scans will show a progression of aberrations.

Point spread function shows how light from a point source will be distorted by the subject's optical system. This scan was done before surgery, without correction.

Getting post-surgery feedback. Dr. Hardten also uses wavefront data to help him decide the best way to improve a patient's vision after treatment. For example, one of Dr. Hardten's patients had a post-LASIK manifest refraction of -0.5, +0.5 x 110 OD; he was 20/20 uncorrected, 20/20 best corrected. However, the patient's "wavefront refraction" showed sphere and cylinder of -0.29, -0.27, axis 23, and that 73% of the problems with his post-op vision were higher-order aberrations, mostly in the form of coma, with a little trefoil.

As it turned out, Dr. Hardten said, this patient is quite happy with his result and reports no significant glare or halos. However, if a patient like this were unhappy with the outcome, the higher-order aberrations would need to be addressed in his retreatment.

Practical concerns

Dr. Hardten noted three practical issues to keep in mind when using wavefront technology:

Pupil size. One of the differences between wavefront technology and corneal topography is that when measuring with wavefront technology, pupil size is important; you can only collect information from the area of the eye in which light rays can go in and out. For that reason, topography is still helpful for getting information about the peripheral cornea, and to help you determine which aberrations come from the cornea, and which come from other structures in the eye (mainly the lens).

Also, Dr. Hardten reports, measured aberrations typically increase as pupil size increases, even in normal eyes, because you pick up more of the peripheral areas of the cornea. (Even a normal cornea isn't a perfect sphere or cylinder.) For that reason, he suggests doing the scans in dim light so you'll have a chance to correct more aberration.

Make sure all test results match. Occasionally, different refractions of the same eye may not agree. For this reason, Dr. Hardten says that he looks at the manifest refraction, the wavefront refraction and the cycloplegic refraction before proceeding with any treatment. If all three don't agree, he tries to determine the reason. If you encounter a discrepancy like this, Dr. Hardten suggests that you repeat the tests, just as you would if your manifest and cycloplegic refractions were a diopter different, or your topography map showed cylinder but your refraction didn't.

Look at the point spread function. The point spread function gives you an idea of what effect the aberration would have if the patient was looking at a point source of light. The sample maps on page 44 show the point spread function in a patient's left and right eyes before surgery, without correction.

Dr. Hardten pointed out that it's very important to note the scale of the point spread function maps when making a comparison. Two similar maps may be displaying a much smaller or larger number of degrees of arc. For example, the top pre-op maps on page 44, showing all aberrations, cover 60 minutes of arc; the lower two maps, showing higher-order aberrations, cover only 4 minutes of arc.

The future has arrived

Although wavefront technology isn't a miracle cure, it's clear that many patients stand to benefit from it, even before wavefront-guided ablations become an approved option in the United States. If you've been thinking about eventually adding wavefront technology to your practice, perhaps eventually should be . . . today.

 

A Brief Glossary of Wavefront Terminology

Wavefront technology allows us to measure aberrations that weren't previously measurable. In order to describe them in a meaningful way, surgeons and scientists have had to create new terms. During his presentation, John A. Vukich, M.D., clarified the meaning of some of the most common terms used when discussing wavefront:

Zernike polynomials. These are three-dimensional shapes that represent the solutions to different polynomial equations; they provide a convenient way to quantify the components of optical blur. These mathematically perfect shapes don't represent actual "warps" in someone's optical system. Instead, they allow us to analyze a complex "actual shape" by treating it as if it were made up of a mix of mathematically perfect shapes, much like analyzing a stew by quantifying each of its ingredients.

Most important, wavefront technology allows us to mathematically "remove" the distortion relating to one shape and consequently measure the distortion that remains. For example, we can mathematically eliminate the distortion caused by sphere and cylinder and quantify the remaining higher-order aberrations.

Optical path difference. As you know, wavefront systems project parallel rays of light into the eye and measure their displacement when they reflect back out. The displacement (i.e., the optical path difference) is mathematically translated into a number that correlates (via a simple mathematical ratio) to the corneal height that needs to be removed to create a "flat" wavefront reading. In a wavefront map, these numbers are translated into colors, producing the characteristic patterns that you see.

Root mean square (RMS). Optical path difference varies from point to point. However, for practical reasons you need to characterize and quantify the whole visual field. The RMS value is a single number that characterizes how extreme the variances are over the whole visual field. It can be calculated for a single category of distortion or total distortion.

To determine how extreme the distortion is, you can't simply add up the values above and below the "ideal" plane and calculate the arithmetic mean. Because some are positive and some are negative, the values will cancel each other out. So, to ensure that we're adding positive numbers, all values are squared. Then these numbers are averaged; RMS is the square root of that average. This number gives us an idea of how serious the aberrations being measured are.

Coefficients. Zernike polynomials represent the solutions of equations. Coefficients are key numbers in those equations, and they happen to reflect how much of a given aberration is present in the measured optical system. Thus, a coefficient is another number that, like RMS, can be used to indicate how prominent a given aberration is.

Coma. One of the two Zernike third-order aberrations. It consists of a bulge above the reference plane and a bulge below the reference plane, adjacent to each other but on opposite sides of the visual field. Put another way, it represents a myopic area across from a hyperopic area. (In a point spread function map, coma may look like a comet -- hence the name.)

Because both "bulges" have a central point, and two points determine a line, you can speak about coma having an axis, like astigmatism.

Trefoil. The other third-order aberration. This shape is reminiscent of cylinder, but with three axes coming out from a center point (like a pinwheel) instead of the single axis found in regular astigmatism. This type of aberration probably explains why some patients appear to have more than one solution when you attempt to determine the axis of their astigmatism.

Spherical aberration. This is the central shape in the fourth order level of the pyramid of Zernike polynomials. (It's sometimes called the sombrero hat, which it resembles.) It appears to be much more common than the other fourth-order shapes, and seems to be a significant contributor to blur; hence it's been given a name of it's own.

Point spread function. This function describes how the light from a single point would be scattered on the retina by the patient's optical system. (See image on page 44.) Two useful measures are the percentage of light subtended within a given circle of arc on the retina, and the Strehl ratio, which compares the actual spread to a theoretical ideal.

-- John A. Vukich, M.D.

 

Dr. Schallhorn discussed a study that examined the higher aberrations of top gun pilots at the Navy Fighter Weapons School. The study found little difference in level of higher aberrations between individuals with excellent vision and those with average vision. In fact, some comparisons indicated that people with less sphere and cylinder -- i.e., better uncorrected vision -- had significantly more higher aberrations, as measured by RMS. The higher-order aberrations most likely to be present in this group were vertical coma and, to a lesser extent, spherical aberration.

However, Dr. Schallhorn pointed out that "excellent vision" in this study was determined using standard, high-contrast eye charts. When the pilots' vision was compared using a low-contrast chart, even though the results weren't statistically significant, pilots with less higher-order aberration tended to have better contrast detection than pilots with more higher-order aberrations.

Standard LASIK can cause significant increases in higher-order aberrations. Dr. Schallhorn discussed data from 100 consecutive patients treated with nonwavefront-guided LASIK, using the latest algorithms. Ninety percent of patients were 20/20 or better uncorrected following surgery, but higher-order aberrations were significantly increased. The study also found that the increased RMS correlated with lower contrast sensitivity.

Much of the increase in higher-order aberration was accounted for by spherical aberrations, and higher levels of spherical aberration correlated with more halo symptoms and glare complaints. (In contrast, an increase in coma or trefoil didn't correlate with halo symptoms.)

Dr. Schallhorn also noted another interesting fact: Eyes with more spherical aberration before surgery showed the greatest increase in spherical aberration after treatment.

The ablation, not the flap, induces spherical aberration. Dr. MacRae reported a study of 18 patients in which a flap was made and checked for 2 months prior to lifting the flap and ablating. Making the flap, by itself, produced almost no increase in spherical aberration.

At the same time, he pointed out, his and other studies have shown a correlation between amount of myopia corrected and the amount of spherical aberration induced. Both results suggest that the ablation, not the flap, causes the increase in aberration.

Investigating Higher-Order Aberrations

Wavefront technology is slowly revealing more about higher-order aberrations. Here are some recent discoveries that were mentioned during the ASCRS presentation:

Higher-order aberrations are stable over time. Steve C. Schallhorn, M.D., reported on studies designed to check the accuracy of wavefront measurement. One study measured the same patients day after day to check for measurement consistency. The study found little variation between higher-order aberration measurements over time, which suggests not only that the wavefront readings are reliable, but that the aberrations themselves are consistent over time.

Not all aberrations are equally disruptive. Scott MacRae, M.D., reported that David Williams, M.D., at the University of Rochester in New York, has an adaptive optic system that allows him to correct out (or add in) higher-order aberrations when refracting a patient. To determine the relative amount of distortion caused by different higher-order aberrations, Dr. Williams had students increase the amount of different aberrations until they reached a standard level of blur.

He found that aberrations that fall near the middle of the pyramid of Zernike polynomials, such as coma and secondary astigmatism, tend to be much more disruptive. (Dr. MacRae noted that these shapes produce more distortion in the central portion of the wavefront, rather than out toward the edge.)

Dr. Schallhorn reported similar findings from clinical studies.

Fifth-order aberrations are rare, but disruptive. Dr. MacRae reported that a study of 200 nonsurgical and 40 symptomatic postsurgical eyes found that significant fifth-order aberration (secondary astigmatism and secondary coma) was rare in nonsurgical eyes. The predominant higher-order aberrations in nonsurgical eyes were third-order aberrations, and most of this aberration was coma. However, in postoperative symptomatic eyes, fifth-order aberrations, if present, tended to be accompanied by more severe visual complaints.

Changing the angle of an existing aberration is very disruptive. According to Dr. MacRae, Dr. Williams and Pablo Artal, M.D., at the University of Mucia in Spain, have demonstrated that if a patient is accustomed to vertical coma, for example, adding horizontal coma causes much more visual difficulty than adding a similar amount of vertical coma.

Aberrations aren't necessarily bad. Several presenters offered evidence of this counter-intuitive possibility:

Dr. MacRae reported that adding a certain amount of spherical aberration to myopia can sometimes produce a clearer image. So in some cases, a higher RMS may mean better acuity, not worse.

 

What to Read Next